Concept 6: Proximal Policy Optimization (PPO)
Proximal Policy Optimization (PPO)
ℹ️ Definition Proximal Policy Optimization (PPO) is a policy gradient algorithm that constrains policy updates to stay within a "trust region", preventing destructively large policy changes and enabling stable, sample-efficient learning.
Learning Objectives
By the end of this lesson, you will:
- Understand why large policy updates cause instability
- Learn the PPO clipped objective and trust region concept
- Implement PPO from scratch using PyTorch
- Use Stable-Baselines3 for production PPO agents
- Apply PPO to continuous control and Atari games
- Tune PPO hyperparameters for optimal performance
Introduction
In Lessons 4-5, we learned policy gradient methods:
- REINFORCE: High variance, unstable
- Actor-Critic: Lower variance, but still sensitive to learning rate
Problem: One bad update can destroy a good policy.
Example:
vbnet
Step 1000: Policy performs well (reward = 200)
Step 1001: Large gradient update due to noisy batch
Step 1002: Policy completely broken (reward = 10)
Step 1003-∞: Can't recover from bad policy
PPO Solution: Constrain updates to small changes -> stable learning.
The Problem with Vanilla Policy Gradients
Trust Region Intuition
Think of policy optimization as hiking in fog:
- Current policy: Where you're standing
- Gradient: Direction that looks promising
- Problem: Gradient is estimated from limited samples (foggy!)
Vanilla PG: Take a big step in gradient direction (might walk off cliff) PPO: Take small, conservative steps (stay safe)
Why Large Updates Fail
python
# Old policy: π_old(a|s) = [0.4, 0.3, 0.3]
# New policy: π_new(a|s) = [0.9, 0.05, 0.05]
#
# Problem: Drastically different behavior from one update!
# Result: Performance collapse, can't recover
Key Insight: Small policy changes -> predictable performance changes. Large policy changes -> unpredictable chaos.
Trust Region Policy Optimization (TRPO)
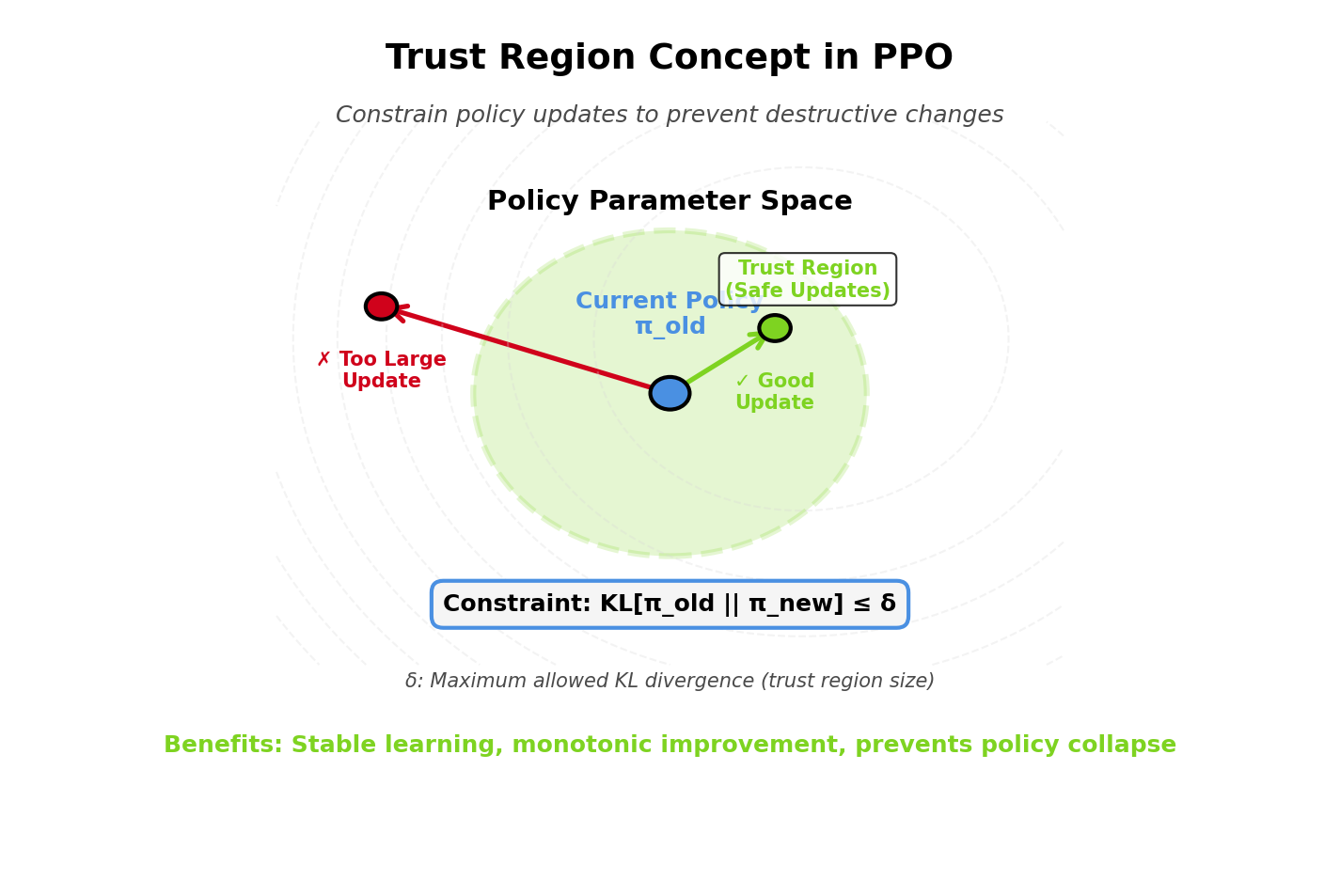
The Trust Region Concept
Idea: Only make updates that satisfy a constraint:
scss
maximize J(θ)
subject to KL(π_θ_old || π_θ) ≤ δ
Where:
- KL(π_θ_old || π_θ): KL divergence between old and new policy
- δ: Trust region size (e.g., 0.01)
- Interpretation: Keep new policy close to old policy
TRPO Algorithm
TRPO enforces trust regions using constrained optimization:
python
# 1. Compute policy gradient
g = estimate_policy_gradient()
# 2. Compute Fisher Information Matrix
F = estimate_fisher_information_matrix()
# 3. Solve constrained optimization (complex!)
θ_new = θ_old + sqrt(2δ/g^T F^{-1} g) * F^{-1} g
Problem: Computing F^-1 is expensive and complex.
PPO: Approximate trust regions with a simpler clipped objective!
PPO: Simplified Trust Regions
The PPO Objective
Instead of explicit KL constraint, PPO uses a clipped surrogate objective:
scss
L^CLIP(θ) = E_t [min(r_t(θ) * A_t, clip(r_t(θ), 1-ε, 1+ε) * A_t)]
Where:
- r_t(θ): Probability ratio = π_θ(a_t|s_t) / π_θ_old(a_t|s_t)
- A_t: Advantage at time t
- ε: Clipping parameter (typically 0.2)
Understanding the Probability Ratio
Probability ratio:
c
r_t(θ) = π_θ(a_t|s_t) / π_θ_old(a_t|s_t)
Interpretation:
- r_t = 1: New policy = old policy (no change)
- ``r_t > 1``: New policy more likely to take action a_t
- ``r_t < 1``: New policy less likely to take action a_t
Example:
python
# Old policy: π_old(action=RIGHT | state) = 0.3
# New policy: π_new(action=RIGHT | state) = 0.6
# Ratio: r = 0.6 / 0.3 = 2.0
# Interpretation: New policy 2× more likely to go right
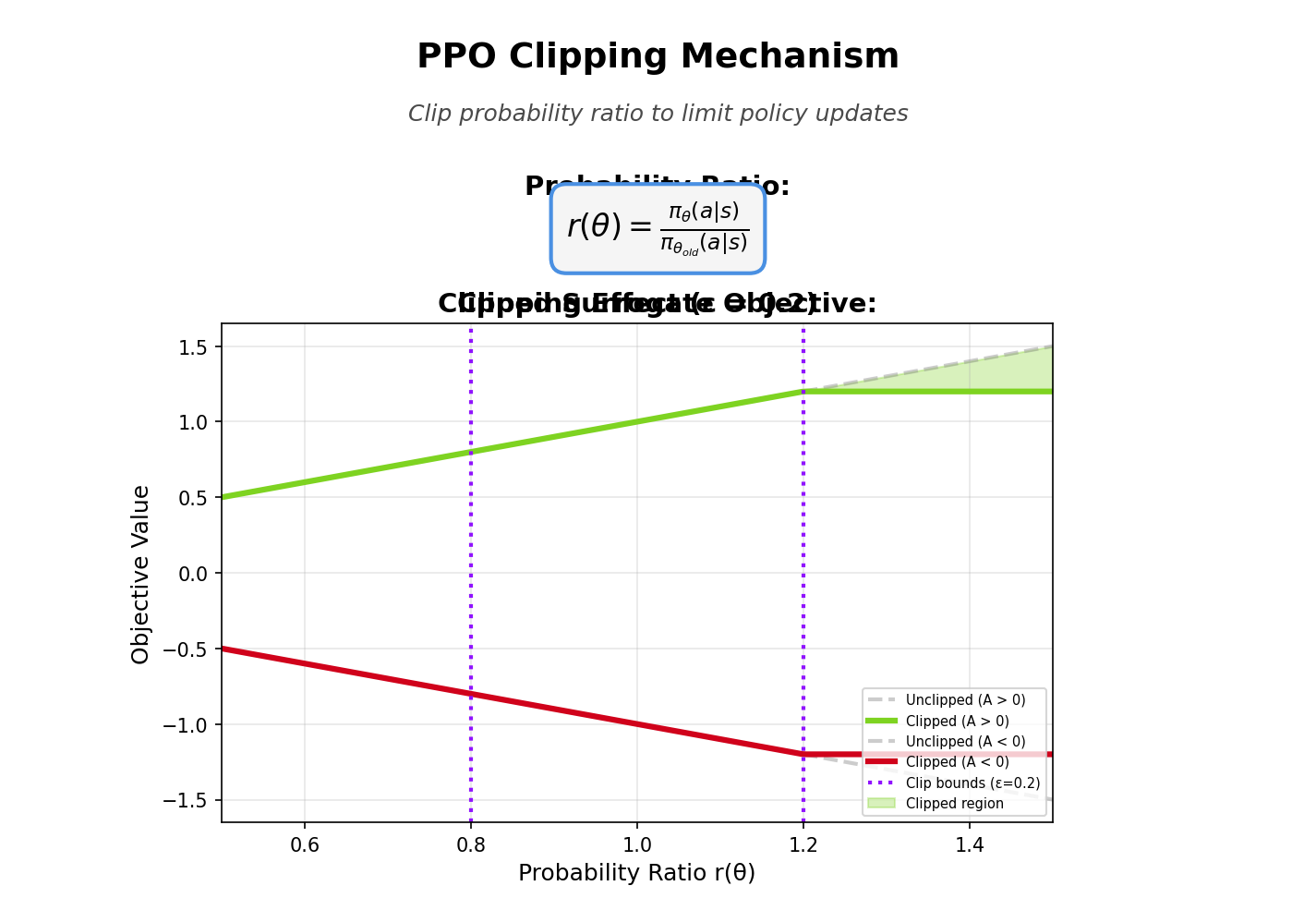
The Clipping Mechanism
Unclipped objective (vanilla policy gradient):
scss
L(θ) = r_t(θ) * A_t
PPO clipped objective:
scss
L^CLIP(θ) = min(r_t(θ) * A_t, clip(r_t(θ), 1-ε, 1+ε) * A_t)
What clip() does:
python
clip(r, 1-ε, 1+ε):
if r < 1-ε: return 1-ε # Clip from below
if r > 1+ε: return 1+ε # Clip from above
else: return r # No clipping
Clipping Visualization
With ε = 0.2:
yaml
Advantage > 0 (good action):
━━━━━━━━━━━━━━━━━━━━━━━━━━━━
r_t < 0.8: No incentive to decrease π(a|s) further (clipped at 0.8)
0.8 ≤ r_t ≤ 1.2: Proportional reward
r_t > 1.2: No incentive to increase π(a|s) further (clipped at 1.2)
Advantage < 0 (bad action):
━━━━━━━━━━━━━━━━━━━━━━━━━━━━
r_t < 0.8: No incentive to decrease π(a|s) further (clipped at 0.8)
0.8 ≤ r_t ≤ 1.2: Proportional penalty
r_t > 1.2: No incentive to increase π(a|s) further (clipped at 1.2)
Effect: Prevents large changes in policy (trust region).

Why Clipping Works
Case 1: Positive Advantage (``A_t > 0``)
css
# Good action, want to increase probability
# But clip at r = 1.2 prevents excessive increase
L^CLIP = min(r * A, 1.2 * A) for r > 1.2
└─────┘ └────┘
Unclipped Clipped (no further gain)
Case 2: Negative Advantage (``A_t < 0``)
css
# Bad action, want to decrease probability
# But clip at r = 0.8 prevents excessive decrease
L^CLIP = min(r * A, 0.8 * A) for r < 0.8
└─────┘ └────┘
Unclipped Clipped (no further gain)
PPO Algorithm (Complete)
python
Initialize actor π(a|s; θ) and critic V(s; w)
Set hyperparameters: ε, K (epochs), M (minibatch size)
for iteration in range(num_iterations):
# 1. Collect trajectories using π_θ_old
trajectories = []
for _ in range(num_actors):
τ = collect_trajectory(env, π_θ_old, T_steps)
trajectories.append(τ)
# 2. Compute advantages using critic
for τ in trajectories:
advantages = compute_gae(τ, critic, γ=0.99, λ=0.95)
returns = advantages + values # TD target
# 3. PPO update (K epochs on same data)
for epoch in range(K):
# Shuffle and create minibatches
for minibatch in random_shuffle(trajectories):
states, actions, old_log_probs, advantages, returns = minibatch
# Compute probability ratio
new_log_probs = log π_θ(actions | states)
ratio = exp(new_log_probs - old_log_probs)
# Clipped surrogate objective
surr1 = ratio * advantages
surr2 = clip(ratio, 1-ε, 1+ε) * advantages
actor_loss = -mean(min(surr1, surr2))
# Value function loss
values = V(states; w)
critic_loss = mean((returns - values)²)
# Entropy bonus (optional)
entropy = -mean(probs * log(probs))
# Total loss
loss = actor_loss + 0.5 * critic_loss - 0.01 * entropy
# Update networks
update(actor, critic, loss)
Key Features
- Multiple epochs: Train on same batch multiple times (K=10 typical)
- Clipped objective: Prevents large policy changes
- Minibatch updates: More stable than full-batch
- Shared network: Actor and critic can share layers (optional)
PPO Implementation (PyTorch)
python
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical
class ActorCritic(nn.Module):
def __init__(self, state_dim, action_dim):
super().__init__()
# Shared feature extractor
self.shared = nn.Sequential(
nn.Linear(state_dim, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU()
)
# Actor head
self.actor = nn.Linear(128, action_dim)
# Critic head
self.critic = nn.Linear(128, 1)
def forward(self, state):
features = self.shared(state)
logits = self.actor(features)
value = self.critic(features)
return logits, value
def get_action_and_value(self, state):
logits, value = self.forward(state)
probs = torch.softmax(logits, dim=-1)
dist = Categorical(probs)
action = dist.sample()
log_prob = dist.log_prob(action)
entropy = dist.entropy()
return action, log_prob, value, entropy
# Training
def ppo_update(model, optimizer, states, actions, old_log_probs, returns, advantages,
clip_epsilon=0.2, epochs=10, batch_size=64):
for _ in range(epochs):
# Shuffle data
indices = torch.randperm(len(states))
for i in range(0, len(states), batch_size):
batch_indices = indices[i:i+batch_size]
# Get current policy and value
logits, values = model(states[batch_indices])
probs = torch.softmax(logits, dim=-1)
dist = Categorical(probs)
# Compute new log probs
new_log_probs = dist.log_prob(actions[batch_indices])
# Compute ratio
ratio = torch.exp(new_log_probs - old_log_probs[batch_indices])
# Clipped surrogate objective
advantages_batch = advantages[batch_indices]
surr1 = ratio * advantages_batch
surr2 = torch.clamp(ratio, 1 - clip_epsilon, 1 + clip_epsilon) * advantages_batch
actor_loss = -torch.min(surr1, surr2).mean()
# Value function loss
returns_batch = returns[batch_indices]
critic_loss = nn.functional.mse_loss(values.squeeze(), returns_batch)
# Entropy bonus
entropy = dist.entropy().mean()
# Total loss
loss = actor_loss + 0.5 * critic_loss - 0.01 * entropy
# Update
optimizer.zero_grad()
loss.backward()
nn.utils.clip_grad_norm_(model.parameters(), max_norm=0.5)
optimizer.step()
PPO with Stable-Baselines3
Why Stable-Baselines3?
Production-ready implementation with:
- Optimized performance
- Automatic hyperparameter scheduling
- Built-in logging and visualization
- Support for parallel environments
Installation
bash
pip install stable-baselines3[extra]
Basic Usage
python
from stable_baselines3 import PPO
from stable_baselines3.common.env_util import make_vec_env
# Create vectorized environment (4 parallel environments)
env = make_vec_env('CartPole-v1', n_envs=4)
# Create PPO agent
model = PPO(
"MlpPolicy", # Policy architecture
env,
learning_rate=3e-4,
n_steps=2048, # Steps per environment before update
batch_size=64,
n_epochs=10, # PPO epochs per update
gamma=0.99,
gae_lambda=0.95,
clip_range=0.2,
verbose=1
)
# Train
model.learn(total_timesteps=100000)
# Save
model.save("ppo_cartpole")
# Load and test
model = PPO.load("ppo_cartpole")
obs = env.reset()
for _ in range(1000):
action, _ = model.predict(obs, deterministic=True)
obs, reward, done, info = env.step(action)
Advanced Configuration
python
from stable_baselines3 import PPO
from stable_baselines3.common.vec_env import SubprocVecEnv
from stable_baselines3.common.callbacks import CheckpointCallback
# Custom policy network
policy_kwargs = dict(
net_arch=[dict(pi=[256, 256], vf=[256, 256])] # Separate actor/critic
)
# Checkpoint callback
checkpoint_callback = CheckpointCallback(
save_freq=10000,
save_path='./checkpoints/',
name_prefix='ppo_model'
)
# Create model
model = PPO(
"MlpPolicy",
env,
policy_kwargs=policy_kwargs,
learning_rate=lambda progress: 3e-4 * progress, # Linear decay
clip_range=lambda progress: 0.2 * progress, # Adaptive clipping
verbose=1,
tensorboard_log="./ppo_tensorboard/"
)
# Train with callbacks
model.learn(
total_timesteps=1000000,
callback=checkpoint_callback
)
Hyperparameters
Critical Hyperparameters
| Parameter | Typical Value | Effect |
|---|---|---|
| Clip range (ε) | 0.1 - 0.3 | Larger: more aggressive updates |
| Learning rate | 3e-4 | Standard for PPO |
| N-steps | 128 - 2048 | Steps before update (more = more stable) |
| Batch size | 32 - 256 | Minibatch size for updates |
| N-epochs | 3 - 10 | Training epochs per batch |
| GAE λ | 0.9 - 0.99 | Advantage estimation smoothness |
| Entropy coefficient | 0.01 | Exploration bonus |
Tuning Guidelines
For simple environments (CartPole):
python
learning_rate = 3e-4
n_steps = 128
batch_size = 64
n_epochs = 4
clip_range = 0.2
For Atari:
python
learning_rate = 2.5e-4
n_steps = 128
batch_size = 256
n_epochs = 4
clip_range = 0.1 # More conservative
For continuous control (MuJoCo):
python
learning_rate = 3e-4
n_steps = 2048
batch_size = 64
n_epochs = 10
clip_range = 0.2
PPO for Continuous Actions
Gaussian Policy
python
class ContinuousPPO(nn.Module):
def __init__(self, state_dim, action_dim):
super().__init__()
self.shared = nn.Sequential(
nn.Linear(state_dim, 128),
nn.ReLU(),
nn.Linear(128, 128),
nn.ReLU()
)
self.mean = nn.Linear(128, action_dim)
self.log_std = nn.Parameter(torch.zeros(action_dim))
self.critic = nn.Linear(128, 1)
def forward(self, state):
features = self.shared(state)
mean = self.mean(features)
std = torch.exp(self.log_std)
value = self.critic(features)
return mean, std, value
def get_action_and_value(self, state):
mean, std, value = self.forward(state)
dist = torch.distributions.Normal(mean, std)
action = dist.sample()
log_prob = dist.log_prob(action).sum(dim=-1)
entropy = dist.entropy().sum(dim=-1)
return action, log_prob, value, entropy
Monitoring PPO Training
Key Metrics
Policy metrics:
- policy_loss: Should decrease initially, then stabilize
- approx_kl: KL divergence (should stay small,
<0.02) - clip_fraction: Fraction of samples clipped (0.1-0.3 is good)
Value metrics:
- value_loss: Should decrease
- explained_variance: How well critic predicts returns (>0.5 is good)
Performance:
- episode_reward: Average episode return (should increase)
- episode_length: Average episode length
Using TensorBoard
python
model = PPO("MlpPolicy", env, tensorboard_log="./ppo_logs/")
model.learn(total_timesteps=100000)
# View logs
# tensorboard --logdir ./ppo_logs/
Common Issues
Issue 1: Policy Not Learning
Symptoms: Reward doesn't increase, policy stays random.
Diagnostics:
- Check
approx_kl-> should ``be > 0.001`` (policy is updating) - Check
explained_variance-> should ``be > 0`` (critic learning)
Fixes:
- Increase learning rate
- Increase clip range (0.2 -> 0.3)
- Increase n_epochs (4 -> 10)
Issue 2: Training Unstable
Symptoms: Reward oscillates wildly, sometimes collapses.
Diagnostics:
- Check
approx_kl-> ``if >0.05``, updates too large - Check
clip_fraction-> ``if >0.5``, clipping too frequent
Fixes:
- Decrease learning rate
- Decrease clip range (0.2 -> 0.1)
- Decrease n_epochs (10 -> 4)
- Add gradient clipping
Issue 3: Sample Inefficient
Symptoms: Requires millions of samples to learn simple task.
Fixes:
- Increase n_steps (128 -> 2048) for more data per update
- Increase batch_size (64 -> 256)
- Use parallel environments (n_envs=8)
Advantages of PPO
- Stable: Clipping prevents catastrophic updates
- Sample efficient: Multiple epochs on same data
- Simple: No complex second-order optimization (vs TRPO)
- Robust: Works well with default hyperparameters
- Versatile: Discrete and continuous actions, images and vectors
Limitations of PPO
- On-policy: Can't reuse old data (unlike DQN)
- Hyperparameter sensitive: Performance varies with settings
- Slower than SAC/TD3: For continuous control
- Needs many samples: Compared to model-based RL
Real-World Applications
OpenAI Five (Dota 2)
- Training: 10,000 years of gameplay per day
- Architecture: PPO with 4096 LSTM units
- Performance: Beat professional human team
Robotics
- Manipulation: Pick and place, assembly
- Locomotion: Walking, running, obstacle navigation
- Success: PPO widely used in sim-to-real transfer
Game Playing
- Hide and Seek (OpenAI): Emergent tool use
- Minecraft: Complex long-horizon tasks
- StarCraft II: Partially observable strategy game
Key Takeaways
- PPO constrains policy updates with clipped surrogate objective
- Clipping prevents large, destructive policy changes (trust regions)
- Multiple epochs enable data reuse for sample efficiency
- Robust to hyperparameters, works well with defaults
- Stable-Baselines3 provides production-ready implementation
- Gold standard for policy optimization in RL
Looking Ahead
PPO is widely considered the "gold standard" for policy optimization, but RL has many more techniques:
- Lesson 7: Multi-armed bandits and exploration
- Lesson 8: Debugging and deploying RL agents
- Lessons 9-15: Generative AI fundamentals
- Lesson 16: RLHF combines PPO with language models!
Summary
- PPO uses clipped surrogate objective to constrain policy updates to trust regions
- Probability ratio r_t = π_new(a|s) / π_old(a|s) measures policy change
- Clipping at (1-ε, 1+ε) prevents excessive policy updates
- Multiple epochs on same data improves sample efficiency
- Stable-Baselines3 provides production implementation with monitoring
- Hyperparameters (clip range, learning rate, n_steps) significantly affect performance
- PPO is the most popular policy gradient algorithm for continuous control and robotics