Concept 11: Generative Adversarial Networks (GANs)
Generative Adversarial Networks (GANs)
ℹ️ Definition Generative Adversarial Networks (GANs) are generative models that train two neural networks in competition: a generator that creates fake samples and a discriminator that distinguishes real from fake, resulting in highly realistic sample generation through adversarial training.
Learning Objectives
By the end of this lesson, you will:
- Understand the GAN framework (generator, discriminator, adversarial game)
- Learn the minimax objective and Nash equilibrium
- Implement a GAN for MNIST digit generation using PyTorch
- Diagnose and fix common GAN training failures (mode collapse, instability)
- Apply techniques for stable GAN training
- Compare GANs with VAEs for image generation
Introduction
In Lesson 10, we learned VAEs - generative models with stable training but blurry outputs. GANs take a radically different approach: instead of maximizing likelihood, two networks compete in an adversarial game.
Result: State-of-the-art sample quality, but challenging to train!
GAN Applications:
- Photorealistic face generation (ThisPersonDoesNotExist.com)
- Image-to-image translation (pix2pix, CycleGAN)
- Style transfer and artistic creation
- Super-resolution (enhance image quality)
- Data augmentation for ML training
The GAN Framework
Two-Player Game
Generator (G):
- Goal: Create fake samples that fool the discriminator
- Input: Random noise z ~ N(0, I)
- Output: Fake sample G(z)
- Analogy: Counterfeiter creating fake money
Discriminator (D):
- Goal: Distinguish real samples from fake
- Input: Sample x (real or fake)
- Output: Probability D(x) ∈ [0, 1] that x is real
- Analogy: Police detecting counterfeit money
Training: Generator and discriminator improve simultaneously through competition.
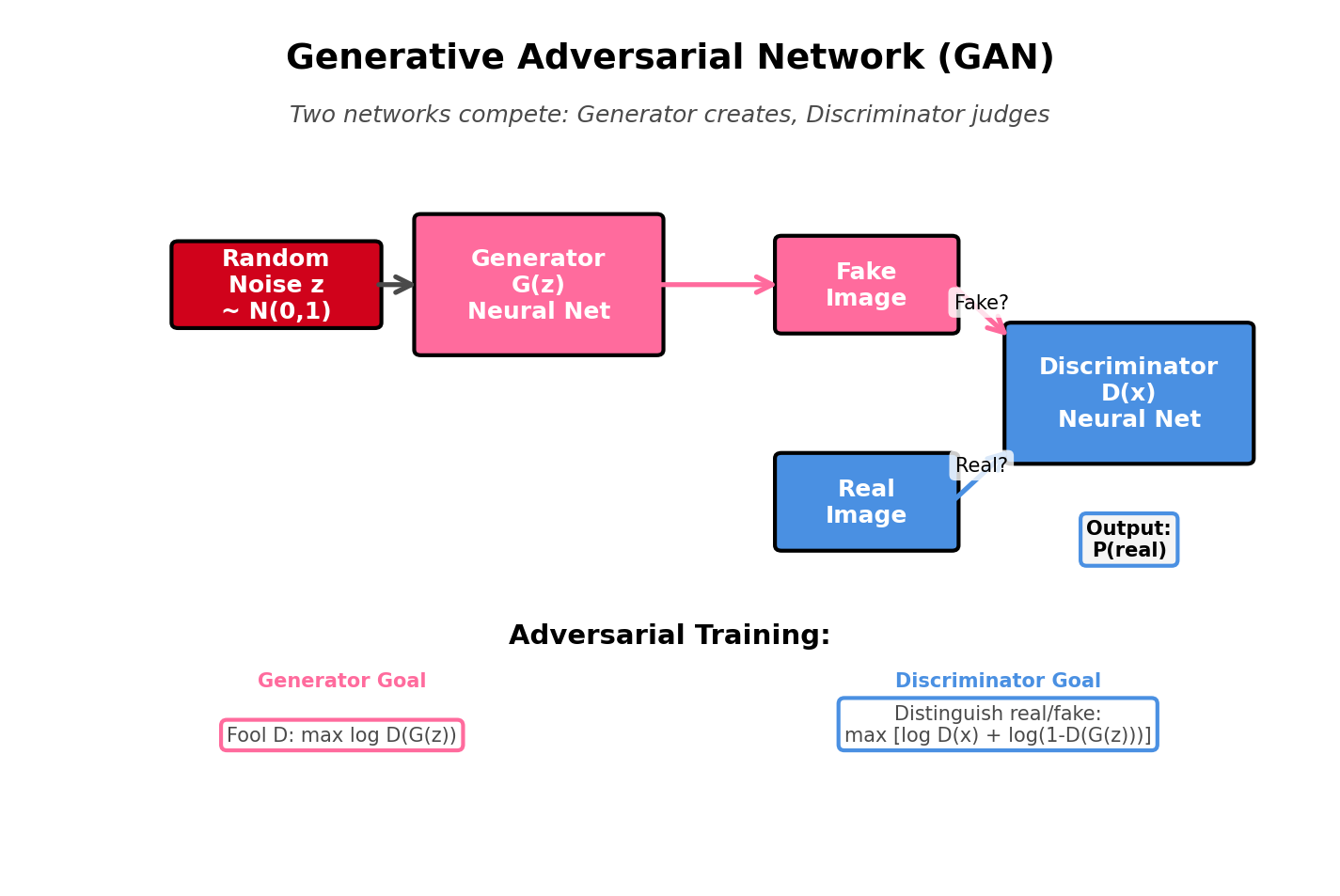
Adversarial Training Loop
css
1. Discriminator trains to distinguish real from fake
- Real samples from training data → Label 1 (real)
- Fake samples from generator → Label 0 (fake)
2. Generator trains to fool discriminator
- Generate fake samples
- Want discriminator to output 1 (thinks they're real)
3. Repeat until Nash equilibrium
Visual Analogy
yaml
Round 1:
Generator: Creates obvious fakes
Discriminator: Easily spots fakes (100% accuracy)
Round 100:
Generator: Creates better fakes
Discriminator: Still catching most fakes (80% accuracy)
Round 10,000:
Generator: Creates photorealistic fakes
Discriminator: Can't reliably distinguish (50% accuracy = random guessing)
↑
Nash equilibrium: Generator wins!
The Minimax Objective
Mathematical Formulation
GAN objective:
scss
min_G max_D V(D, G) = E_x[log D(x)] + E_z[log(1 - D(G(z)))]
Interpretation:
-
Discriminator maximizes:
- log D(x): Correctly identify real samples as real
- log(1 - D(G(z))): Correctly identify fake samples as fake
-
Generator minimizes:
- log(1 - D(G(z))): Fool discriminator into thinking fakes are real
Discriminator Training
Loss function:
bash
L_D = -[E_x[log D(x)] + E_z[log(1 - D(G(z)))]]
In practice:
python
# Real samples
real_loss = F.binary_cross_entropy(D(real_images), torch.ones_like(D(real_images)))
# Fake samples
fake_images = G(noise)
fake_loss = F.binary_cross_entropy(D(fake_images.detach()), torch.zeros_like(D(fake_images)))
d_loss = real_loss + fake_loss
Key: Use .detach() to prevent gradients flowing to generator during discriminator update.
Generator Training
Original objective:
ini
L_G = E_z[log(1 - D(G(z)))]
Problem: Vanishing gradients when D is confident (D(G(z)) ~= 0)
Better objective (non-saturating):
ini
L_G = -E_z[log D(G(z))]
Implementation:
python
fake_images = G(noise)
g_loss = F.binary_cross_entropy(D(fake_images), torch.ones_like(D(fake_images)))
Interpretation: Train generator to maximize probability that discriminator thinks fakes are real.
GAN Architecture
Generator
Input: Random noise z (latent code) Output: Generated sample G(z)
MNIST Generator Example:
python
class Generator(nn.Module):
def __init__(self, latent_dim=100):
super().__init__()
self.model = nn.Sequential(
nn.Linear(latent_dim, 256),
nn.LeakyReLU(0.2),
nn.Linear(256, 512),
nn.LeakyReLU(0.2),
nn.Linear(512, 1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 784), # 28x28 = 784
nn.Tanh() # Output in [-1, 1]
)
def forward(self, z):
img = self.model(z)
return img.view(-1, 1, 28, 28)
Discriminator
Input: Sample x (real or fake) Output: Probability D(x) that x is real
MNIST Discriminator Example:
python
class Discriminator(nn.Module):
def __init__(self):
super().__init__()
self.model = nn.Sequential(
nn.Linear(784, 512),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(512, 256),
nn.LeakyReLU(0.2),
nn.Dropout(0.3),
nn.Linear(256, 1),
nn.Sigmoid() # Output probability
)
def forward(self, img):
img_flat = img.view(img.size(0), -1)
validity = self.model(img_flat)
return validity
Complete GAN Training Loop
python
import torch
import torch.nn as nn
import torch.optim as optim
# Initialize models
latent_dim = 100
generator = Generator(latent_dim)
discriminator = Discriminator()
# Optimizers
g_optimizer = optim.Adam(generator.parameters(), lr=0.0002, betas=(0.5, 0.999))
d_optimizer = optim.Adam(discriminator.parameters(), lr=0.0002, betas=(0.5, 0.999))
# Loss function
criterion = nn.BCELoss()
# Training loop
for epoch in range(num_epochs):
for i, (real_images, _) in enumerate(dataloader):
batch_size = real_images.size(0)
# Real and fake labels
real_labels = torch.ones(batch_size, 1)
fake_labels = torch.zeros(batch_size, 1)
# ---------------------
# Train Discriminator
# ---------------------
d_optimizer.zero_grad()
# Real images
real_outputs = discriminator(real_images)
d_real_loss = criterion(real_outputs, real_labels)
# Fake images
z = torch.randn(batch_size, latent_dim)
fake_images = generator(z)
fake_outputs = discriminator(fake_images.detach()) # Detach!
d_fake_loss = criterion(fake_outputs, fake_labels)
# Total discriminator loss
d_loss = d_real_loss + d_fake_loss
d_loss.backward()
d_optimizer.step()
# -----------------
# Train Generator
# -----------------
g_optimizer.zero_grad()
# Generate fake images
z = torch.randn(batch_size, latent_dim)
fake_images = generator(z)
fake_outputs = discriminator(fake_images)
# Generator loss (fool discriminator)
g_loss = criterion(fake_outputs, real_labels) # Want D(G(z)) = 1
g_loss.backward()
g_optimizer.step()
print(f"Epoch [{epoch}/{num_epochs}], d_loss: {d_loss.item():.4f}, g_loss: {g_loss.item():.4f}")
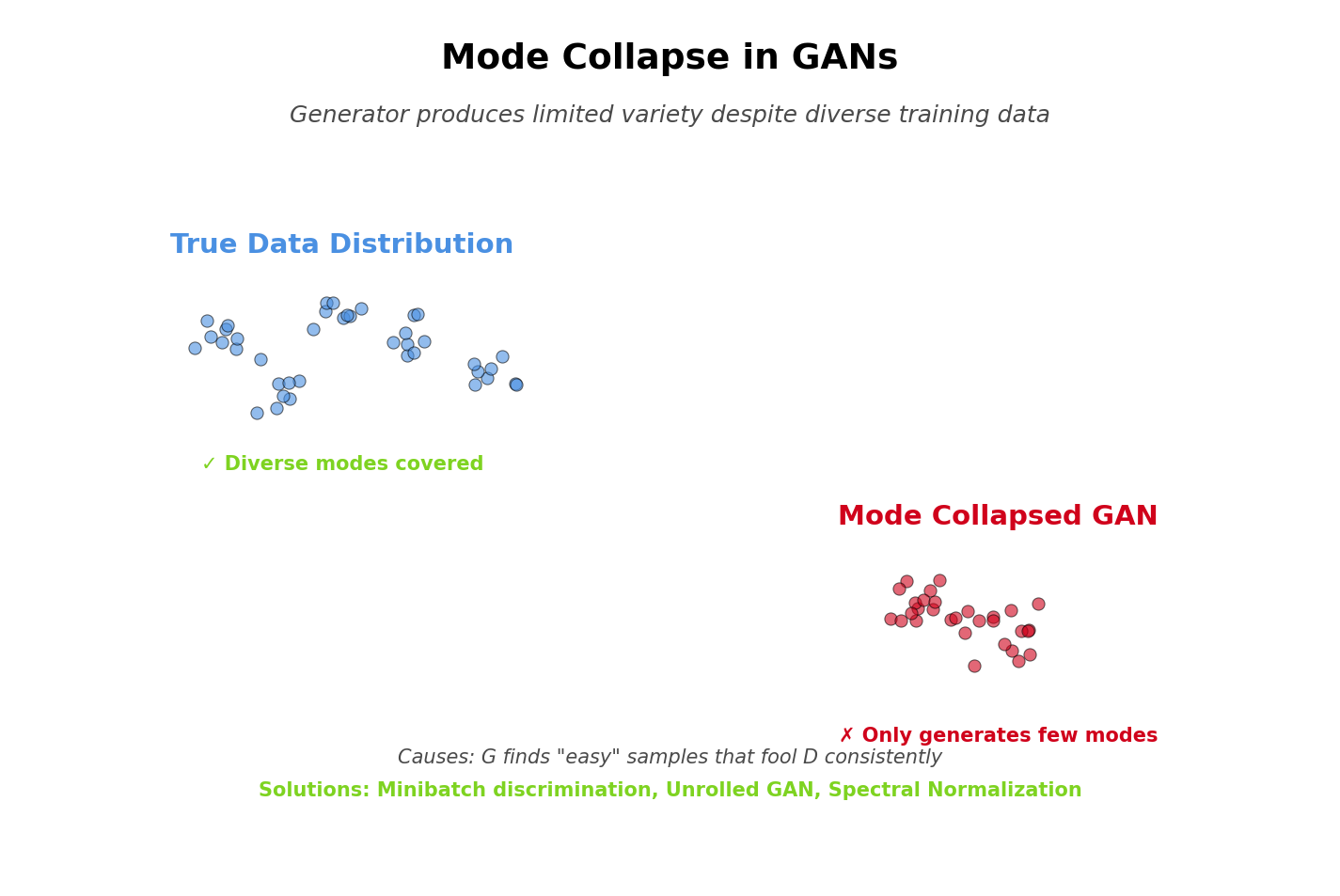
Common GAN Training Failures
One. Mode Collapse
Problem: Generator produces limited variety of samples
Symptoms:
- All generated samples look very similar
- Generator ignores parts of latent space
- Diversity metric (FID, IS) degrades
Causes:
- Generator finds a few samples that fool discriminator
- Stops exploring other modes of data distribution
Solutions:
- Minibatch discrimination: Discriminator sees multiple samples at once
- Feature matching: Match statistics of real/fake features
- Unrolled GAN: Look ahead to prevent mode collapse
- Use different GAN variant: WGAN, LSGAN
2. Training Instability
Problem: Losses oscillate wildly, training diverges
Symptoms:
- Generator loss explodes or vanishes
- Discriminator loss goes to 0 (perfect discrimination)
- Generated samples degrade over training
Causes:
- Learning rates too high
- Discriminator too strong (generator can't improve)
- Vanishing gradients
Solutions:
- Lower learning rates: Try 0.0001-0.0002
- Balance discriminator/generator: Train D less frequently
- Label smoothing: Use 0.9 instead of 1.0 for real labels
- Gradient penalty: WGAN-GP adds gradient norm constraint
3. Vanishing Gradients
Problem: Generator stops learning
Symptoms:
- Generator loss plateaus
- Generated samples don't improve
- Discriminator achieves near-perfect accuracy
Causes:
- Discriminator too strong
- Saturating loss function
Solutions:
- Non-saturating loss: Use -log D(G(z)) instead of log(1 - D(G(z)))
- Wasserstein GAN: Different loss function
- Spectral normalization: Constrain discriminator Lipschitz constant
4. Convergence Failure
Problem: Training doesn't converge to Nash equilibrium
Symptoms:
- Losses don't stabilize
- Sample quality plateaus far from realistic
Causes:
- Poor hyperparameters
- Architecture mismatch
- Inappropriate loss function
Solutions:
- Careful hyperparameter tuning
- Progressive training: Start low-res, gradually increase
- Self-attention: Capture long-range dependencies
- Try proven architectures: DCGAN, StyleGAN
Techniques for Stable GAN Training
One. Label Smoothing
Problem: Hard labels (0, 1) can cause overconfidence
Solution: Smooth labels
python
real_labels = torch.ones(batch_size, 1) * 0.9 # Instead of 1.0
fake_labels = torch.zeros(batch_size, 1) + 0.1 # Instead of 0.0
2. Noisy Labels
Add noise to discriminator inputs:
python
# Add Gaussian noise to real and fake images
noise = torch.randn_like(real_images) * noise_std
noisy_real = real_images + noise
noisy_fake = fake_images + noise
Decay noise over training:
python
noise_std = initial_noise * (decay_rate ** epoch)
3. One-Sided Label Smoothing
Only smooth real labels:
python
real_labels = torch.rand(batch_size, 1) * 0.1 + 0.9 # [0.9, 1.0]
fake_labels = torch.zeros(batch_size, 1) # Keep at 0
4. Feature Matching
Match statistics of intermediate features:
python
# Extract features from discriminator
real_features = discriminator.get_features(real_images)
fake_features = discriminator.get_features(fake_images)
# Generator loss: match feature statistics
g_loss = F.mse_loss(fake_features.mean(0), real_features.mean(0))
5. Historical Averaging
Penalize deviation from historical parameters:
python
g_loss_gan = criterion(fake_outputs, real_labels)
g_loss_history = F.mse_loss(generator.parameters(), historical_params)
g_loss = g_loss_gan + lambda_history * g_loss_history
6. Experience Replay
Train discriminator on mix of current and past fake samples:
python
# Store past fake samples
if len(replay_buffer) < buffer_size:
replay_buffer.append(fake_images.detach())
else:
replay_buffer[random.randint(0, buffer_size-1)] = fake_images.detach()
# Train discriminator on mix
past_fakes = random.sample(replay_buffer, batch_size // 2)
current_fakes = fake_images[:batch_size // 2]
mixed_fakes = torch.cat([current_fakes, past_fakes])
DCGAN: Deep Convolutional GAN
Architecture Guidelines
From DCGAN paper (Radford et al., 2015):
- Replace pooling with strided convolutions (discriminator) and fractional-strided convolutions (generator)
- Use batchnorm in both generator and discriminator
- Remove fully connected hidden layers
- Use ReLU in generator except output (Tanh)
- Use LeakyReLU in discriminator for all layers
DCGAN Generator
python
class DCGANGenerator(nn.Module):
def __init__(self, latent_dim=100, channels=1):
super().__init__()
self.model = nn.Sequential(
# Input: latent_dim x 1 x 1
nn.ConvTranspose2d(latent_dim, 512, 4, 1, 0, bias=False),
nn.BatchNorm2d(512),
nn.ReLU(True),
# State: 512 x 4 x 4
nn.ConvTranspose2d(512, 256, 4, 2, 1, bias=False),
nn.BatchNorm2d(256),
nn.ReLU(True),
# State: 256 x 8 x 8
nn.ConvTranspose2d(256, 128, 4, 2, 1, bias=False),
nn.BatchNorm2d(128),
nn.ReLU(True),
# State: 128 x 16 x 16
nn.ConvTranspose2d(128, channels, 4, 2, 1, bias=False),
nn.Tanh()
# Output: channels x 32 x 32
)
def forward(self, z):
return self.model(z.view(-1, z.size(1), 1, 1))
DCGAN Discriminator
python
class DCGANDiscriminator(nn.Module):
def __init__(self, channels=1):
super().__init__()
self.model = nn.Sequential(
# Input: channels x 32 x 32
nn.Conv2d(channels, 128, 4, 2, 1, bias=False),
nn.LeakyReLU(0.2, inplace=True),
# State: 128 x 16 x 16
nn.Conv2d(128, 256, 4, 2, 1, bias=False),
nn.BatchNorm2d(256),
nn.LeakyReLU(0.2, inplace=True),
# State: 256 x 8 x 8
nn.Conv2d(256, 512, 4, 2, 1, bias=False),
nn.BatchNorm2d(512),
nn.LeakyReLU(0.2, inplace=True),
# State: 512 x 4 x 4
nn.Conv2d(512, 1, 4, 1, 0, bias=False),
nn.Sigmoid()
# Output: 1 x 1 x 1
)
def forward(self, img):
return self.model(img).view(-1, 1)
Conditional GAN (cGAN)
Motivation
Problem: Standard GAN can't control what to generate
Solution: Condition both networks on labels/attributes
Architecture
Generator:
css
G(z, y) → x
Discriminator:
css
D(x, y) → probability x is real given label y
Implementation
python
class ConditionalGenerator(nn.Module):
def __init__(self, latent_dim=100, n_classes=10):
super().__init__()
self.label_emb = nn.Embedding(n_classes, n_classes)
self.model = nn.Sequential(
nn.Linear(latent_dim + n_classes, 256),
nn.LeakyReLU(0.2),
nn.Linear(256, 512),
nn.LeakyReLU(0.2),
nn.Linear(512, 1024),
nn.LeakyReLU(0.2),
nn.Linear(1024, 784),
nn.Tanh()
)
def forward(self, z, labels):
# Concatenate noise and label embedding
label_input = self.label_emb(labels)
gen_input = torch.cat([z, label_input], dim=1)
img = self.model(gen_input)
return img.view(-1, 1, 28, 28)
Usage
Generate specific digits:
python
z = torch.randn(10, latent_dim)
labels = torch.LongTensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]) # One of each digit
generated_digits = generator(z, labels)
Evaluation Metrics
One. Inception Score (IS)
Measures: Quality and diversity
Formula:
less
IS = exp(E_x[KL(p(y|x) || p(y))])
Interpretation:
- High IS: Generated images are clear (low entropy p(y|x)) and diverse (high entropy p(y))
- Range: 1 (worst) to ∞
- MNIST: ~10-11, ImageNet: ~200+
2. Fréchet Inception Distance (FID)
Measures: Similarity to real data distribution
Formula:
ini
FID = ||μ_r - μ_g||² + Tr(Σ_r + Σ_g - 2√(Σ_r Σ_g))
Where μ, Σ are mean and covariance of Inception features
Interpretation:
- Lower FID: Closer to real data
- Range: 0 (perfect) to ∞
- Best GANs: ``FID < 10``
3. Mode Score
Measures: Mode coverage (diversity)
Detects: Mode collapse
GANs vs VAEs
| Aspect | GANs | VAEs |
|---|---|---|
| Sample Quality | Sharper, more realistic | Blurry, averaged |
| Training Stability | Unstable, requires tricks | Stable, principled |
| Likelihood | No explicit likelihood | Explicit (ELBO) |
| Mode Coverage | Prone to mode collapse | Covers all modes |
| Latent Space | Less interpretable | Smooth, interpretable |
| Speed | Fast sampling | Fast sampling |
| Use Case | Image generation | Compression, anomaly detection |
Applications
One. Image Generation
- Faces (ThisPersonDoesNotExist.com)
- Bedrooms (LSUN dataset)
- Artwork (Artbreeder)
2. Image-to-Image Translation
- pix2pix: Edges -> Photos
- CycleGAN: Horses <-> Zebras
- StarGAN: Multi-domain translation
3. Super-Resolution
- SRGAN: Enhance image resolution
- ESRGAN: Even better super-resolution
4. Text-to-Image
- StackGAN: Text descriptions -> Images
- AttnGAN: Attention-based text-to-image
5. Data Augmentation
- Generate training data for ML models
- Rare event simulation
Key Takeaways
- GANs train generator and discriminator in adversarial game
- Minimax objective defines competition between G and D
- Training challenges: Mode collapse, instability, vanishing gradients
- Stable training techniques: Label smoothing, feature matching, experience replay
- DCGAN architecture provides guidelines for stable CNN-based GANs
- Conditional GANs enable controlled generation
- Trade-offs: Better sample quality than VAEs, but harder to train
Looking Ahead
- Lesson 12: Advanced GAN architectures (StyleGAN, Progressive GAN, CycleGAN)
- Lesson 13: Diffusion models (current state-of-the-art for image generation)
- Project 3: GAN Art Studio (create your own GAN-generated artwork)
Summary
- GANs use adversarial training between generator and discriminator
- Generator creates fake samples, discriminator judges real vs fake
- Minimax objective defines the adversarial game
- Training challenges: Mode collapse, instability, vanishing gradients
- DCGAN provides architectural guidelines for stable training
- Conditional GANs enable controlled generation with labels
- Evaluation: Inception Score, FID, mode coverage metrics
- Trade-off: Superior sample quality, but more difficult to train than VAEs